レンズ
レンズは被写体の像をセンサー上に作る働きを持つ,カメラでもっとも重要な部品の一つです.レンズには凸レンズと凹レンズがありますが,写真撮影用のレンズ(写真レンズ)は全体として凸レンズの働きをします.凸レンズはその一方にある物体の像を、反対側に上下左右反転して投影する性質があり,その像をセンサーで記録することが写真の撮影です.
写真レンズも虫眼鏡のレンズも,「凸レンズ」という意味では同じ機能をもったレンズです.写真レンズを覗けば物が大きく見えますし,虫眼鏡でも被写体の像を作ることは可能です.ただし,虫眼鏡で作ることができる被写体の像は歪んでいたり,部分的にボケていたり,色が滲んでいるなどあまり綺麗ではありません.これらは様々な要因であらゆるレンズに生じてしまう現象で,「収差」と呼ばれています.このような収差を極力少なくするために色々な工夫をしてあるのが写真レンズです.例えば異なった性質を持ったガラスで作った,形もそれぞれ異なる複数のレンズを上手く組み合わせることで,ある程度収差をなくすことができます.このような工夫がレンズメーカーの腕の見せ所であり,また収差の残り加減がレンズの善し悪しを左右する重要な要素でもあります.一方で収差の残り加減はレンズの個性でもあり,レンズの「味」と表現されるなど,ある程度の収差は逆に歓迎されることもあるのが面白いところです.
実際の写真レンズにはこのような収差がある程度あるのは避けられませんし,全くの無収差がレンズの「理想」とも言い切れないのは上記の通りです.しかし,今後の説明図では簡単のために,このような収差を全く持たない「理想的な」レンズが1枚だけあるものとします.
レンズの基本的性質
結像
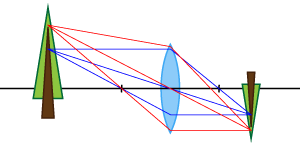
上記の通りレンズは,物体から出て一方から入った光を屈折させて,もう一方にその物体の像を作る(結像させる)働きを持っています.下図aでは,被写体$AB$の像$A′B′$がレンズの反対側にできています.この像$A′B′$の位置にセンサーを置くことで,その像を記録することができ,この「像の位置にセンサーを置く」作業が「ピント合わせ」です.
図a:レンズは物体の像を,レンズの反対側に上下左右逆に作る
同じレンズで比べた場合,物体がレンズから遠くにあればあるほど,像が出来る位置はレンズの近くになります(図 b).
図b:物体がレンズから離れるほど,像の位置はレンズに近づく
そして物体が無限の彼方にあると仮定したとき,物体から出た光は平行光線としてレンズに入ります.このとき,その物体の像が出来る位置を「焦点」,レンズの主点から焦点までの距離を「焦点距離」と言い,写真レンズではミリメートル(mm)で表されます(図 c).
図c:物体が無限遠に位置すると,像は焦点に集中する
レンズの「主点」とは,ちょうどここで本稿が行っているように,写真レンズ全体を同じ働きをする仮想的な一枚の薄いレンズに置き換えたとき,その仮想的レンズの中心を言います.
実際の写真レンズは複数のレンズが組み合わされており,主点は前側主点と後側主点の2つあります。2つの主点の位置も必ずしもレンズの中心にはありませんので,例えば写真レンズの長さとその焦点距離は普通一致しません.
レンズの焦点はレンズの両側にあります.図 cのように平行な光がレンズの左から入れば右側の焦点に光が集まり,逆に光がレンズの右から入れば,左側の焦点に光が集まります.また,焦点から光が出てレンズに当たるとき,光は図と逆の道筋を辿り,平行な光線となって出て行きます.そこで,図を左右逆に眺めて,図の物体と像の位置関係を逆にしても,この図は成り立ちます.例えば図 aの$A’B’$の位置に物体を置けば,$AB$の位置に像が出来ます.レンズに物体を近づけると,像が出来る位置がレンズから遠ざかっていくのは図 bを左右逆に眺めても同じです.さらに図 cのように物体をどんどんレンズに近づけて焦点Fに置くと,レンズから出た光は平行光線になり,像を結びません.
ところで,図では1点から3本の光線しか出ていませんが,これは作図にあたって分かりやすいように選んだ光線です.まずレンズの軸に対して平行な光線は,屈折したあとレンズの後側焦点を通ります.レンズの前側焦点を通った光は,屈折したあとレンズの軸に平行に進みます.3本の中心の光線は「主光線」と呼ばれる光線です.絞りを絞っていくと,絞りの羽根に遮られた光はセンサーに届かなくなりますが,絞りの中心を通る光線は最後まで残ります.この光線を主光線と呼び,被写体のある一点からでた光線の基準となる光線とされます(図には絞りがありませんが,レンズと同じ大きさに絞りが空いているのと同じ事ですから,絞りの中心はレンズの中心に一致します).実際には主光線もレンズを通る時に屈折するのですが,本稿では「理想的なレンズ」の厚さが無視できる(薄い)として,すべて屈折しない直線で表現しています.またこの3本の光線の他にも,光線は被写体からあらゆる方向に出ており,この3本の光線の間や外側の光線も,図と同じ位置に像を結びます.
焦点距離の違いと結像
次に焦点距離の違いが像の大きさ、あるいは画角にどういう影響を与えるかを見てみましょう。下図dとeはそれぞれ焦点距離の相対的に短いレンズと長いレンズによる結像の様子を表しています.
(d)焦点距離の短いレンズ
(e)焦点距離の長いレンズ
図:レンズの焦点距離の違い
焦点距離が長くなると図eのように像のできる位置がレンズから遠くなり,像も大きくなります.像のできる位置にセンサーを置く,つまりピントを合わせるとレンズとセンサーの距離も長くなります.センサーに写る範囲(画角)はセンサーの両端からレンズの主点(本稿で扱っている「理想的」レンズではレンズの中心)に引いた線のなす角度ですから,レンズからセンサーが離れるほど画角は狭くなり,像も大きくなります.
まり焦点距離の異なるレンズを比べると,焦点距離が短いほど被写体は小さく写り,画角(写真に写る範囲)が広くなります(図d).逆に長いほど被写体が大きく写り,画角が狭くなります(図e).
おおよその目安として焦点距離がセンサーの対角線の長さと同じくらいのレンズを「標準レンズ」,それより短いものを「広角レンズ」,それより長いものを「望遠レンズ」と呼んでいます.風景や室内など,できるだけ広い範囲(画角)のものを写したいときには広角レンズが,野生動物やスポーツ選手など近づきにくいものには望遠レンズが使われるなど,焦点距離は写真レンズの用途を分ける一番大きな要素といえます.
写真レンズ
レンズの中でも写真撮影に使われるものを、写真用レンズあるいは写真レンズと呼びます。写真レンズの一番重要な特性は「焦点距離」と「開放F値」です.この2つの数値でレンズの特徴が決定されると言ってよいでしょう.写真レンズの型番も大抵はこの2つの数値を組み合わせて50mm F1.4 などと決められます.
焦点距離については,遠くのものを大きく写したいときには焦点距離の長い望遠レンズを使い,広い範囲を写し込みたいときには焦点距離の短い広角レンズを使う,というのは前述のとおりです.開放F値はそのレンズで設定できる一番小さい(明るい)F値を表します.F値の選択肢が多い方が表現の幅が広がりますが、絞りを絞ることによってF値は必要なだけ大きくできますので,開放F値は小さいほど優秀と言えます.
開放F値
露出の項での解説の通り,F値とはカメラが光を取り込む度合いを表す数値です.このF値が小さいほど光を取り込む量が大きくなります.ほとんどのレンズは絞りを使ってF値を変化させることができますが,開放F値とはそのレンズが取り得る最も小さいF値を表します.この値には単位がないのでイメージしづらいのですが,この値が半分になると明るさが4倍になります.つまり同じ明るさの環境で撮影するとき,開放F値が半分の大きさのレンズを使えば,シャッタースピードを4倍にできます(このことから、英語圏では開放F値が小さいレンズを「fast lens(速いレンズ)」と表現し,開放F値の大きさのことも“lens speed”と表現します).
また,被写体の背景をぼかした撮影をするには出来るだけ小さいF値で撮影するのですが,このとき開放F値が小さいレンズを使えばより小さいF値を選択することが出来,よりぼかした表現が可能になります.つまり,開放F値が小さいレンズの方がシャッタースピードやボケの表現の幅が広がる,よいレンズであるということができます.
F値
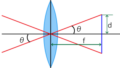
F値には単位がないので直観的に分かりづらいのですが,F値は以下の式で表されます.
$F = \frac{f}{a}$
( $F$:F値 $f$:焦点距離 $a$:開口径 )
開口径とは,レンズの光を通す部分の直径のことです.虫眼鏡のような単純な凸レンズでは開口径はレンズの直径とほぼ同じですが,複数のレンズと絞りを組み合わせた構造の写真レンズの場合は,開口径はレンズを覗いたときに見える絞りの穴(入射瞳)の直径にあたります(絞りを調節することでF値は変化します).式の分母にある開口径$a$を小さくするとF値は大きくなりますが,このことは絞りを絞れば開口径が小さくなり,像は暗くなることを想像すれば納得がいくと思います.
分かりづらいのはなぜ分子に焦点距離$f$が表れるのか,でしょう.焦点距離の説明で触れたとおり,有限の距離にある被写体はレンズから焦点距離$f$よりも離れたところに結像します.その時,$f$が大きくなればなるほど,できる像の大きさも大きくなるのは,例えば図d と図e で解説したとおりです.ですが焦点距離の違うレンズを使っても,開口径が同じならば,もともと入ってくる光の量は同じです.ということは,像が大きくなればなるほど,単位面積あたりの光の量は少なくなります.よって,焦点距離$f$が大きくなればなるほど暗くなるのです.
さて,焦点距離$f$が2倍になれば,像の大きさも2倍になり,像の面積は4倍になりますから,単位面積あたりの光の量は$\frac{1}{4}$になります.一方,開口径$a$が2倍になると,光が通る面積は4倍になりますから,光の量は4倍になります(1点から出てレンズを通った光は1点に結像しますから,レンズを通る光が4倍になれば,結像面にあたる光の量も4倍になります).つまり,明るさは$f$の2乗に反比例し,$a$の2乗に比例することになりますから,$\frac{f}{a}$の2乗に反比例します.$\frac{f}{a}$すなわちF値が2倍になると,明るさは$\frac{1}{4}$になります.
注意深い方はお気づきのように,実際に像の大きさが2倍になるのは,焦点距離ではなくレンズと像の距離が2倍になったときです.レンズと像の距離は,被写体が無限遠にあるときは$f$ですが,それより近い場合は$f$よりも大きくなります.しかし,レンズと被写体との距離を考慮に入れると計算が複雑になるので,一般的にF値の計算からレンズと被写体との距離の影響は省略されています.
ただし,マクロ撮影時など被写体とレンズ(の主点)の距離がかなり近いときには,このような大雑把な計算と実際の明るさとの差が無視できなくなるので,実際の明るさを反映した「実効F値」という値が使われます.詳しくは別の項目で解説しようと思いますが,例えば被写体とレンズの距離が焦点距離の2倍だと実効F値はF値の2倍に,3倍だと1.5倍,6倍だと1.2倍,10倍で1.1倍,100倍で1.01倍くらいになります.仮に焦点距離60mmのレンズを使うとすると,焦点距離の10倍の60cm程度も離れれば,あまり実効F値とF値の差を考慮する必要はないでしょう.それよりも被写体に近づく時には,レンズのF値よりも実際には暗くなることを考慮したほうがいいかもしれません.

コメント