被写界深度の計算

2020.05.10

ボケと被写界深度の項では被写界深度の大まかな性質の説明だけに留めましたが，計算過程の説明も無く多くのグラフを掲載したので，どうしてこうなるの？とモヤモヤした方も多いと思います．そこでここでは少々ややこしく読みづらいのは承知で，被写界深度の計算をしてみましょう．

被写界深度の計算は若干面倒ですが，計算自体は中学数学程度（微分も三角関数も出てきません）なので，段階を踏んで追っていけば問題ありません．ここではまず，ピントが合っている被写体より手前や奥側にある点の像が作る錯乱円の大きさを計算します．そして，被写体からその点が前後にどの程度離れると錯乱円の大きさが許容錯乱円の大きさと一致するかを求めます．手前側と奥側の一致点の間の距離が被写界深度ということになります．

レンズの公式

まず今後の話の前提として，レンズの公式を簡単に説明します．

$A$ $C$ $D$ $F$ $f$ $d_o$ $d_i$ $A’$ $B$ $B’$

図のように被写体$AB$から出た光がレンズを通ってセンサー上に像$A’B’$を結ぶとします．$F$はレンズの焦点，細い実線は光線を表します．するとレンズ（正確には，レンズの主点）と被写体との距離$d_o$，焦点距離$f$，レンズとセンサー上の像との距離$d_i$には，以下の関係が成り立ちます．

$\frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f}$ （レンズの公式）

証明
$\triangle ABC \sim \triangle A’B’C$，$\triangle DCF \sim \triangle A’B’F$から
$d_o : d_i = f : d_i – f$
よって
$d_i f = d_o (d_i – f)$
両辺を $d_i d_o f$ で割ると
$\frac{1}{d_o} = \frac{1}{f} – \frac{1}{d_i}$
移項して
$\frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f}$

錯乱円の大きさ

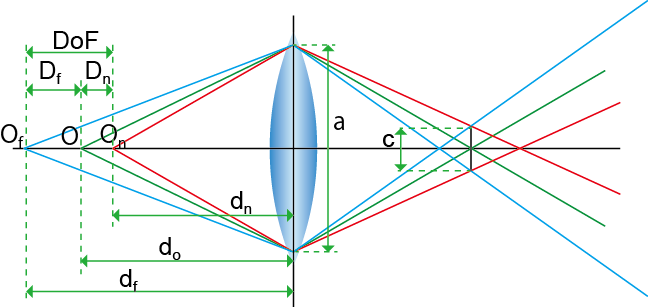
ではまず，錯乱円の大きさを計算しましょう．図はピントの合った被写体$O$とその像$I$，被写体よりレンズに近い点$O_n$とその像の錯乱円の直径$c$を表しています．ここでは$c$は許容錯乱円の大きさと一致している状態と考えるので，被写体よりレンズから遠い点$O_f$の作る錯乱円と大きさとも一致しています．

$O$ $O_n$ $d_n$ $d_o$ $d_c$ $d_i$ $I_n$ $A$ $a$ $c$ $A’$ $B’$ $B$ $I$

ここで，
$\triangle I_nA’B’ \sim \triangle I_nAB$より

$\begin{align} a:c &= d_c : d_c – d_i\\ c d_c &= a(d_c – d_i)\\ c &= a \frac{d_c – d_i}{d_c}\\ \end{align}$

レンズの公式より

\begin{align} d_c &= \frac{d_n f}{d_n – f}\\ d_i &= \frac{d_o f}{d_o – f}\\ \end{align}

これを代入して

\begin{align} c &= a \frac{ \frac{d_n f}{d_n – f} – \frac{ d_o f }{ d_o – f } }{ \frac{d_n f}{ d_n – f } }\\ c &= a \frac{ d_n(d_o – f) – d_o(d_n – f) }{ d_n(d_o – f) }\\ c &= a f \frac{ d_o – d_n }{ d_n(d_o – f) }\\ \end{align}

これを見ると錯乱円の大きさは開口径に比例し，焦点距離が大きくなると錯乱円も大きくなりそうなことが分かります（被写体よりレンズから遠い物体でも同様の計算をすると分子が$d_o – d_n$から $d_f – d_o$ に変わりますが，それ以外は$d_n$が$d_f$に置き換わる他は同じです）．

さらに，$a = \frac{f}{F}$ より，

\begin{align} c = \frac{f^2}{F} \frac{ d_o – d_n }{ d_n(d_o – f) } \end{align}

カメラを扱う上ではこの形の方が分かりやすいと思います．焦点距離に対してカメラから被写体までの距離が十分に大きい($d_o \approx d_o – f$の)時、錯乱円の大きさ，つまりボケの大きさは，焦点距離の2乗に比例しF値に反比例します．例えば焦点距離を2倍にしたとき，ボケ量を同じにするためにはF値をほぼ4倍にすれば良いことになります．

被写界深度の計算

さてここで被写界深度をグラフから読み取るのでは無く，きちんと計算するために，被写界深度を被写体までの距離$d_o$，焦点距離$f$と許容錯乱円の大きさ$c$で表してみましょう．まずレンズからみて被写体より手前にあり，錯乱円の大きさが$c$になる点と被写体との距離$D_n$，同様にレンズから被写体より遠くにあり，錯乱円の大きさが$c$になる点と被写体との距離$D_f$を求め，それを加えて被写界深度とします（図）．

$O$ $O_n$ $O_f$ $D_f$ $DoF$ $D_n$ $d_n$ $d_o$ $d_f$ $a$ $c$

被写体よりレンズに近い場合の錯乱円の大きさ$c$は，

$c = af\frac{d_o – d_n}{d_n(d_o – f)}$

ここで$D_n = d_o – d_n$と置くと，$d_n = d_o – D_n$より

\begin{align} c &= af\frac{D_n}{(d_o – D_n)(d_o-f)} \\ afD_n &= c(d_o^2 – D_n d_o – d_o f + f D_n) \\ D_n(af + cd_o – cf) &= cd_o^2 – d_ocf \\ D_n &= \frac{ cd_o(d_o – f)}{af + cd_o – cf} \\ \end{align}

右辺の分子と分母に$\frac{f}{a}$を掛けると，$\frac{f}{a} = F$(F値)より

\begin{align} D_n &= \frac{d_oFc(d_o – f)}{f^2 + d_oFc – Fcf} \\ D_n &= \frac{d_oFc(d_o-f)}{f^2 + Fc(d_o – f)} \\ \end{align}

一方被写体よりレンズから遠い場合の錯乱円の大きさ$c$は，

$c = af\frac{ d_f – d_o }{ d_f (d_o – f)}$

ここで同様に$D_f = d_f – d_o$と置くと，$d_f = D_f + d_o$より

\begin{align} c &= af\frac{D_f}{(D_f + d_o)(D_o – f)} \\ afD_f &= c(d_o^2 + D_f d_o – f d_o – f D_f) \\ D_f(af – c d_o + fc) &= c d_o^2 – fc d_o \\ D_f &= \frac{cd_o^2 – fcd_o}{af – cd_o + fc} \\ \end{align}

右辺の分子と分母に$\frac{f}{a}$を掛けると，

\begin{align} D_f &= \frac{Fcd_o^2 – fFcd_o}{f^2 -Fcd_o + Fcf}\\ D_f &= \frac{d_oFc(d_o – f)}{f^2 – Fc(d_o – f)} \end{align}

よって被写界深度$DoF$は，

\begin{align} DoF &= D_n + D_f\\ DoF &= \frac{d_oFc(d_o-f)}{f^2 + Fc(d_o – f)} + \frac{d_oFc(d_o – f)}{f^2 – Fc(d_o – f)} \\ DoF &= \frac{2 f^2 d_o F c (d_o – f)}{f^4 – F^2 c^2 (d_o – f)^2} \end{align}

ボケと被写界深度の項のグラフは，上記の計算を経て描かれています．

コメント

タイトルとURLをコピーしました