被写界深度の項では、許容錯乱円の大きさとして35mmフルサイズで一般的に使われている30μm(=0.03mm)を採用しました(APS-Cではこの1/1.5の20μm)。ここで許容錯乱円についておさらいしておきます。(理想的な)レンズによって被写体の像がセンサー上に結像しているとき、被写体上の点はセンサー上でも点として結像します。しかし像の位置がセンサーの位置から前後にずれているとき、被写体上の点はセンサー上では点にならず、ある程度の大きさを持った円になります。この円のことを錯乱円と呼びます。錯乱円の大きさが小さい時は点と区別がつかず、ピントが合っているものと見なせますが、大きくなるにつれてボケとして認識されます。このピントが合っていると認識できる最大の錯乱円を許容錯乱円と呼びます。ただ「ピントが合っていると認識できる」範囲は人や条件によって違い、35mmフルサイズでは30μmがよく使われています。ここではこの30μmという大きさの妥当性について検討してみます。
「ボケている」とはどういうことか
「ボケている」とは、より具体的に言えば、「本来2つに分かれているものが、区別が付かず1つに見えてしまう状態」と言い換えることができます。つまり本来点が2つあるのに繋がって見える、あるいは本来途切れている線が繋がって見える状態が「ボケている」と表現されます。ただ人間の視力には限りがありますから、ここでいう「本来」とは分子レベルまで遡るものではありませんし、そこまでのレベルに言及すればあらゆる写真はボケています。そこで「ある視力をもった人が見て」という但し書きがついて、正確には「ある視力を持った人が見て本来2つに見えるはずのものが、区別がつかず1つに見えてしまう状態」が「ボケている状態」である、と言うことができます。
視力と許容錯乱円
この「ある視力を持った人」の視力が良ければ、より細かい違いが見え「ボケていない状態」の基準が厳しくなりますから、被写界深度は浅くなります。逆に視力の悪い人にとってはその基準が緩いので、同じ写真を見ても被写界深度は深くなります。つまり視力によって被写界深度は変わるのです。では次に許容錯乱円30μmで算出される被写界深度は視力いくつくらいに相当するのか考えてみましょう。
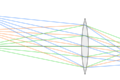
錯乱円の大きさが30μmの時、2つの点を区別できる最短距離を考えます。2つの点それぞれが直径30μmの錯乱円に広がりますので、2つの点の距離が錯乱円の半径の2倍、つまり30μmになったとき2つの錯乱円が繋がってしまい、区別ができなくなります。よってセンサー上の2つの点の距離が許容錯乱円の大きさより大きいとき、2つの点が分かれて見える、つまり「ボケない」と言えます。
さて、日本では一般的にランドルト環を使った視力測定が行われています。ランドルト環による視力測定はCの様な形の輪(ランドルト環)の欠けた部分を判別できるかで行い、1.454mmの隙間を5m離れた所から判別できる視力を1.0としています。これは角度にすると1分(60分の1度)にあたり、0.5分が判別できれば視力2.0、2分までしか判別できなければ視力は0.5とします。
ここで35mmフルサイズの写真を引き伸ばして、24mm x 36mmの大きさのセンサー上の30μmを1.454mmまで拡大したとします。拡大率は約48.5倍ですから、写真の大きさは大体116cm x 174cmになります。この写真を5mの距離から見るとき、視力1.0の人が判別できる距離の限界が1.454mmですから、1.454mm以下のボケは点と区別できず、ピントが合っているように見えます。これは元のセンサー上では30μm以下の錯乱円を点と見なす(許容錯乱円の大きさを30μmとしている)ことに対応しています。つまり許容錯乱円の大きさ30μmで被写界深度を計算することは、視力1.0の人が116cm x 174cmの写真を5mの距離から見た状況をシミュレートしていると言えます。これは角度としてはL版写真(89mm x 127mm)を37cmくらいから、A4版(210mm x 297mm)にすると87cmくらいから見ることに相当します(視力はあくまでも5mの距離から測ることになっているので、近眼の人は5mから見るよりもくっきりと見えるはずです)。87cmは、成人男性が腕を一杯に伸ばした長さよりも大分長いので、ちょっと遠すぎるように感じるかもしれませんが、実際にA4の写真を手に持って眺めてみると、全体を細かく見るのは難しいものです。写真の全体を見る場合には、かなり妥当な設定では無いかと思います。ただ、デジタルの時代になってからモニタ上で等倍鑑賞する機会が増え、ピントに対する基準は随分厳しく言われるようになりました。そのような鑑賞の仕方をする場合には、30μmよりも厳しい基準で評価される事になります。
ピクセルと許容錯乱円
今度は試みに、モニタ上での等倍鑑賞を想定して、意味のある許容錯乱円の最小の大きさを考えてみます。「理想的な」レンズを使う前提で考え得る一番細かい単位は、センサーの画素ピッチです。センサーの画素ピッチより狭い間隔の2点は原理的に判別不能ですから、センサーの画素ピッチがもっとも厳しい許容錯乱円の大きさとなるでしょう。ただし画素ピッチと同じ幅の2点があった場合、センサーの画素上の結像場所によって判別できない場合があります。このことを考慮すると、画素ピッチの2倍~3倍程度が適当かもしれません。
2400万画素の35mmフルサイズセンサーの画素ピッチは約5.8μm、同じく2400万画素のAPS-Cセンサーの画素ピッチは約3.8μmですから、その2倍~3倍とするとフルサイズで30μmの基準の約1/4~2/3程度の大きさになり、計算上の等倍鑑賞での被写界深度は浅くなります。画素数が2倍になると一辺の画素数は約1.41倍になりますから、その分だけ等倍鑑賞での被写界深度も浅くなります。
解像度の限界
センサー製造技術や画像処理技術の発達によって,画素ピッチの小さいセンサーでも以前と比べてノイズが少なくなっていますから,全体として画素数は増加する傾向があることは確かです.しかし,ここで光の波としての性質の問題がでてきます.光はマクロな視点で見たときには,「光線」というように,まっすぐな線と考えられますが,このようなμmサイズで見たときには,回折という現象によって原理的にどうしても光が分散してしまうのです.例えば本来「点」である被写体は,センサー上では円盤状に広がってしまい,この円盤を「エアリーディスク」といいます.エアリーディスクを考慮した分解能(2点を区別できる最小の距離)は光の波長とF値に比例し,$x = 1.22 \lambda F$で表されます.写真に関わる光である可視光の波長は大体0.5μm程度であり,この式に当てはめると分解能はF2のとき約1.2μm,F8で約4.9μm,F16だと約9.8μmになります.F値が大きくなると2点を区別しにくくなるということは,つまり絞ると画像がボケる事になり,これを「小絞りボケ(こしぼりぼけ)」と呼びます。例えば35フルサイズmmフルサイズで2400万画素の時の画素ピッチは約6μm,6000万画素では画素ピッチは約3.8μmですから,F16まで絞ると2400万画素の解像度を生かし切れず,F8でも6000万画素の解像度に到達できません.これ以上画素ピッチを小さくしても,小絞りボケの影響で一定以上絞った時の解像度の上昇は見込めないと考えられます.
イメージするには,方眼紙を塗りつぶして絵を描くことを考えましょう.昔のゲームのドット絵みたいなものです.ここで,塗りつぶすのに使うペンの直径2mmだとすると,方眼が2mmより大きい場合には,方眼を小さくすればするほど細かい絵を作ることが出来ますが,2mmより小さい方眼,例えば1mmの方眼紙を使っても,結局ペンでは4マス同時にしか塗れないので,2mmの方眼を使っているのと実質同じ事になってしまいます.デジカメのセンサーの解像度も,2021年現在それに近い状況にあると言えるでしょう.

コメント